瓜斯拉的逆袭
0%

论文笔记：《Time Interval Aware Self-Attention for Sequential Recommendation》

发表于 更新于 分类于
本文字数： 5k 阅读时长 ≈ 13 分钟

原paper：https://dl.acm.org/doi/10.1145/3336191.3371786

源码解读：https://github.com/Guadzilla/Paper_notebook/tree/main/TiSASRec

中译：时间间隔感知的自注意力序列推荐

总结：是SASRec工作的延续，在self-attention的基础上加了绝对位置信息和相对时间间隔信息（加在Q和K里）取得了更好的performamce。发现Beauty数据集序列模式不明显。

Abstract

  • question作者想解决什么问题？

MC模型和RNN模型都只将用户交互作为有序序列（一种强假设），却没有考虑交互与交互之间的时间间隔。

  • method作者通过什么理论/模型来解决这个问题？

在序列模型的结构中显式建模交互的时间戳（timestamps），并且探索不同时间间隔对next item推荐的影响。提出TiSASRec模型，模型建模了item在序列中的绝对位置以及交互之间的时间间隔。

  • answer作者给出的答案是什么？

展示了不同设定下TiSASRec的特点，比较了不同位置编码下自注意力模块的表现。在dense和sparse数据集都取得了SOTA。

Introduction

  • why作者为什么研究这个课题？

Temporal recommendation（实时推荐）主要建模“绝对时间”来捕获用户与物品的实时动态，即挖掘实时模式、依据时间建模。Sequential recommendation（序列推荐）主要依据交互的顺序挖掘序列模式。序列推荐只用timestamps来决定item顺序，其实假设了所有交互之间是等间隔的。但一天之内产生的序列和一个月内产生的序列显然对next item的影响区别很大。

  • how当前研究到了哪一阶段

目前的序列推荐只挖掘序列模式，即假设交互之间是等间隔的，不合理。有模型使用自注意力+相对位置编码[1]，受到启发。

  • what作者基于什么样的假设（看不懂最后去查）

交互序列应该被建模为包含时间间隔的序列。

Conclusion

  • 优点

    • 结合了绝对位置编码和相对时间间隔编码的优点。
    • 证明了使用相对时间间隔的有效性。

  • 缺点

  • 展望

Dataset & Metric

  • 数据来源

    • MovieLens-1m
    • Amazon CDs&Vinyl/ Movies&TV/ Beauty/ Games
    • Steam

  • 重要指标

    • Hit@10、NDCG@10

Method & Table

  • 模型架构

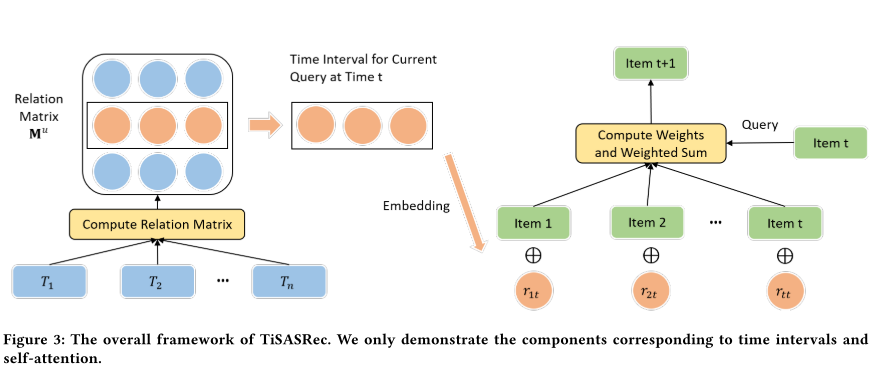
  • 参数说明

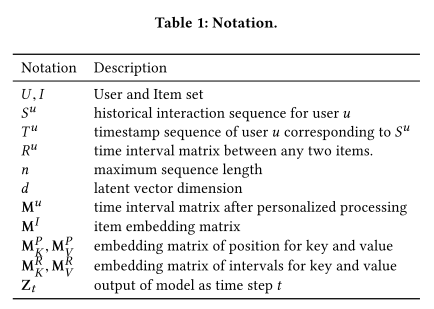
image-20211116223530787

1.个性化的时间间隔（time interval）

规定了序列$S$的maxlen（n），长度小于n的序列用一个特殊标记的padding item来padding。时间序列$T$用第一个item的timestamps来padding（到这里还只是时间戳）。

对每个用户制定个性化的时间间隔，个性化指的其实就是下面介绍的缩放操作。对用户$u$来说，时间戳序列$t=(t_1,t_2,…,t_n)$，用任意两个物品的时间戳之差表示物品之间的时间间隔，作为任意两个物品之间的关系（relation）$r_{ij}$，于是得到时间间隔集合$R^u$。规定一个缩放系数$r^u_{min}=min(R^u)$，即序列里的最小时间间隔，再对所有时间间隔缩放$r^u_{ij}=\lfloor\frac{|r_i-r_j|}{r^u_{min}}\rfloor$，得到时间间隔矩阵$M^u\in N^{n\times n}$。

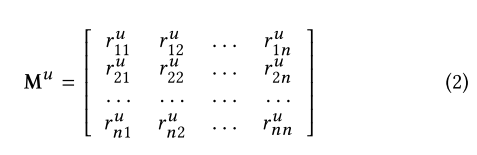
image-20211116225152019

另外，论文还规定了每个$r^u_{ij}$的阈值，对大于阈值的做了一个clip操作得到$M^u_{clipped}$。

2.Embedding层

  • item的表示：padding item用$\vec0$表示，其它每个item用d维向量表示，构成$M^I\in R^{|I|\times d}$的item embedding矩阵，则前n个item的表示为$E^I\in R^{n\times d}$。

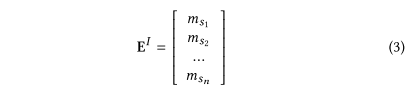
image-20211117222616679

  • position 的表示：即位置编码，用两个K、V矩阵$M^P_K\in R^{n\times d}$和$M^P_V\in R^{n\times d}$，表示每个位置（序列最大长度为n）的Key和Value向量，分别为$E^P_K\in R^{n\times d}$和$E^P_V\in R^{n\times d}$。

image-20211117081419839

  • relative time interval的表示：和positional embedding相似，用两个K、V矩阵$E^P_K\in R^{k\times d}$和$E^P_V\in R^{k\times d}$，表示每个位置（序列最大长度为n）的Key和Value向量，其中k表示一共有k种相对时间间隔。于是clipped后的$M^u_{clipped}$，把对应的$r_{ij}$替换成对应的K、V向量，就得到了$E^R_K\in R^{n\times n\times d}$和$E^R_V\in R^{n\times n\times d}$。

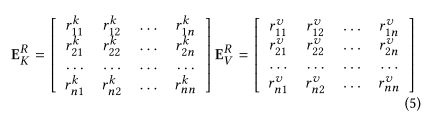
image-20211117081413089

3.时间间隔感知的自注意力机制

仅有item和对应的时间戳也不能把序列确定下来，还要加入item在序列中的位置。

  • 时间间隔感知的自注意力层Time Interval-Aware Self-attention Layer

传统的自注意力层为QKV模式，可以定义成$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V$。用item embedding乘以$W^Q、W^K、W^V$投影到其对应的$Querry、Key、Value$空间上。

这里本质上也是这么做的，但对K和V做了一点改变。

作者首先将$E^I=(m_{s_1},m_{s_2},…,m_{s_n})$表示的item序列变换新序列$Z=(z_1,z_2,…,z_n)$，$z_i\in R^d$。

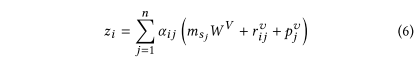
image-20211117222727853

其中$(m_{s_j}W^V+r_{ij}^v+p_j^v)$对应QKV模式里的$Value$，其中$m_{s_j}W^Q$是将item embedding投影到$Value$空间，不过在此基础上还加上了realation embedding（相对时间间隔）和position embedding（位置编码）的value表示。

找到$Value$以后，公式就可以写成：$z_i=\sum^n_{j=1}\alpha_{ij}\ Value_j$。

系数$\alpha_{ij}$是其实就是$softmax(\frac{QK^T}{\sqrt{d_k}})$部分。$softmax()$在论文中体现在$\alpha_{ij}=\frac{exp\ e_{ij}}{\sum^n_{k=1}exp\ e_{ik}}$，那么可以猜测$\frac{QK^T}{\sqrt{d_k}}$就对应论文中的$e_{ij}$了。事实正如此，$e_{ij}$被定义为：

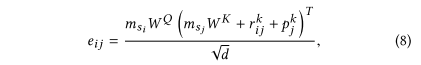
image-20211117090739720

其中$m_{s_j}W^Q$是将item embedding投影到$Querry$空间，对应QKV模式里的$Querry$。

$(m_{s_j}W^K+r^k_{ij}+p^k_j)$，对应QKV模式里的$Key$，其中$m_{s_j}W^K$是将item embedding投影到$Key$空间，不过在此基础上还加上了realation embedding（相对时间间隔）和position embedding（位置编码）的key表示，另外除以的$\sqrt{d}$是缩放系数。

  • 因果关系Causality

序列本身就有因果关系，因为我们在预测第t+1个物品时，只知道前t个物品的信息。但是在做self-attention时，每个物品都能感知到所有物品（因为Q对所有K做了查询），破坏了因果关系。所以我们必须规定，在做self-attention时，规定每个$Q_i$只能查询$K_j$，其中$j<i$，即每个Q只能查询在其之前（previous）的K，满足了因果关系，代码里可以用mask实现。

  • 前馈层Point-wise Feef-Forward Network

FFN为模型加入非线性性。

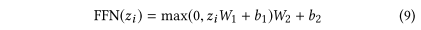
image-20211117093429227

Residual connection和dropout正则化。

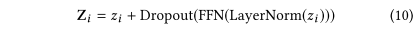
image-20211117093655881

Layer Norm正则化。

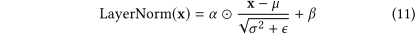
image-20211117093809122

4.预测层

常规的点积计算每个物品的得分。

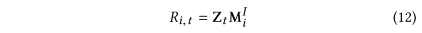
image-20211117094112160

5.模型训练

取物品序列$\widetilde{S_{|S^u|}}=(S^u_1,S^u_2,…,S^u_{|S^u|})$和对应的时间序列$\widetilde{T_{|T^u|}}=(T^u_1,T^u_2,…,T^u_{|T^u|})$的前$|S^u|-1$项，即$\widetilde{S_{|S^u|-1}}=(S^=u_1,S^u_2,…,S^u_{|S^u|-1})$和$\widetilde{T_{|T^u|-1}}=(T^u_1,T^u_2,…,T^u_{|T^u-1|})$。通过裁剪和补长各自化成成相同长度n的两个序列$s=(s_1,s_2,…,s_n)$，和$t=(t_1,t_2,…,t_n)$。给定这两个序列，再规定对应的输出序列$o=(o_1,o_2,…,o_n)$，其中$o_i$定义为：

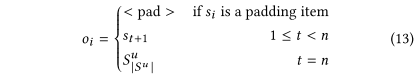
image-20211117095415283

简而言之，padding项的输出为\；$s$最后一项之前的输出（预测）为下一项；$s$最后一项的输出（预测）为$S^u_{|S^u|}$，注意$S^u_{|S^u|}$不在$s$里，因为一开始就把最后一项拿出来了。

loss采用进行负采样的binary cross entropy，加入了F正则项：

image-20211117100703091

padding项也计算了loss，但是没有意义，所以实际计算时把padding项的loss mask掉。

Experiment & Table

1.模型表现

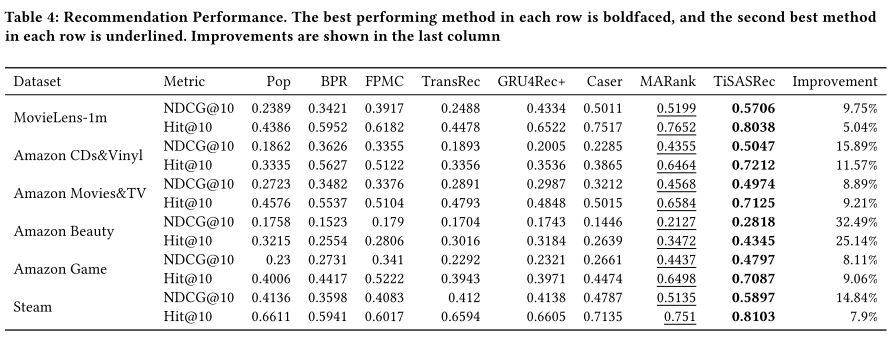
image-20211117101056812

  • TiSASRec在6个数据集上达到了SOTA

2.Ablation Study

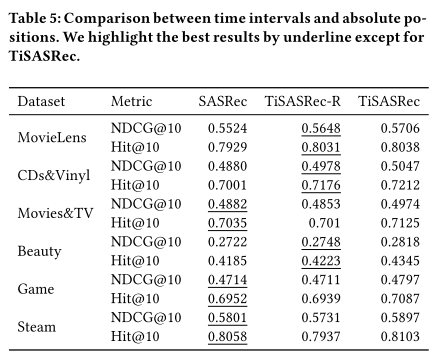
image-20211117103132511

  • TiSASRec-R去掉了在K和V里去掉了position embedding（绝对位置）

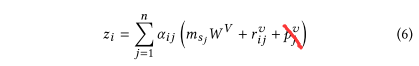
image-20211117103534252

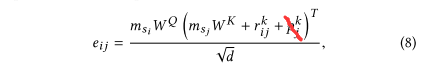
image-20211117103553274

  • SASRec去掉了relative time interval（relation，相对时间间隔）

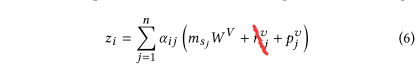
image-20211117114708312

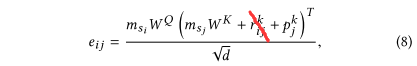
image-20211117114729528

  • 结果表明保留绝对位置和相对时间间隔时model performance最好

3.超参数实验

A.隐向量维度d

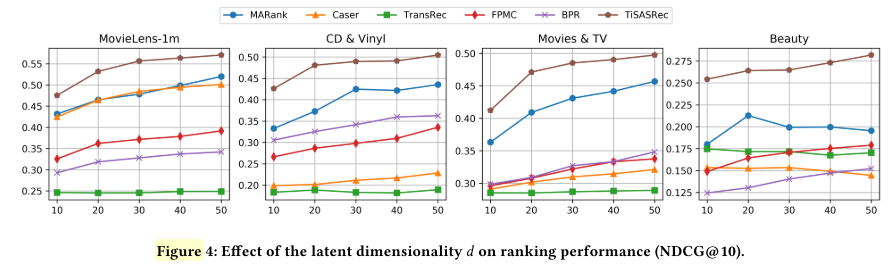
image-20211117104027269

  • 不同模型在不同数据集（除了Games和Steam，why？）上选择d={10，20，30，40，50}
  • 基本上所给模型在所给数据集上都是d越大越好
  • 在Beauty数据集比较特殊，MARank、Caser、TransRec的表现随着d增大在变差
  • 所以最后选d=50

B. 序列最大长度n

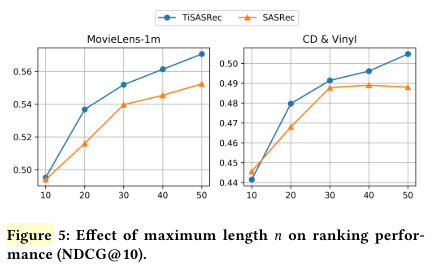
image-20211117104705615

  • n越大效果越好，并且在这两个数据集上SASRec表现比TiSASRec差且更快收敛。
  • 所以最后选n=50
  • 疑问：只选了MovieLens和Amazon CD&Vinyl做实验，why？SASRec论文里选MovieLens-1m做实验的时候maxlen选的可是200，且performance比TiSASRec选50时好….这篇论文maxlen选的最大才50，why？

C.最大时间间隔k

image-20211117105425551

  • k越大意味着要训练的参数越多
  • TiSASRec整体上更稳定，TiSASRec-R当k取合适时表现最好，但当k更大时表现变差。
  • 疑问：ml-1m上比较稳定且permformance在提升，到最大值2048。但CD&Vinyl上最好表现是k=256，但论文最后选的k=512

4.个性化时间间隔实验

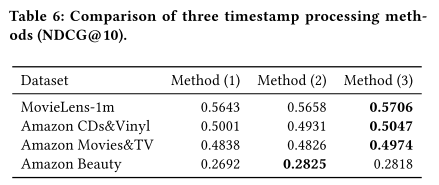
image-20211117110513024

  • Method（1）直接用时间戳作为特征，Method（2）使用没缩放的时间间隔，Method（3）使用个性化（根据每个用户最小时间间隔缩放后的）的时间间隔，即论文方法。
  • 注意前两个方法没有使用时间戳裁剪 timestamps clip
  • Method（3）的performence最好

5.可视化

image-20211117111955529

  • Figure 7 表明预测时使用时间间隔产生的推荐不一样，而且好像更准确
  • Figure 8 是不同时间间隔的权重可视化
    • 小时间间隔的权重更大，说明更短期交互的物品对预测结果影响更大
    • (a)MovieLens是dense数据集，(b) CDs&Vinyl是sparse数据集。左边绿的区域更大，说明dense数据集上预测需要更大范围的物品。
    • Amazon Beauty数据集没有明显的黄绿区域，说明这个数据集没有明显的序列模式，这也说明了为什么有些序列模型在该数据集上效果不是很好。

参考文献

[1]Self-Attention with Relative Position Representations)