论文笔记：《GAG：Global Attributed Graph Neural Network for Streaming Session-based Recommendation》

原paper：GAG: Global Attributed Graph Neural Network for Streaming Session-Based Recommendation

源码解读：（近期发布）

中译：基于流会话推荐的全局属性图神经网络

总结：将SSRM的encoder部分换成了图神经网络模型，并且沿用了NARM、SRGNN等采用的注意力机制，将用户信息作为全局信息融入GNN模型中，解决了保存用户长期兴趣的问题；改进了reservior的采样策略：计算推荐结果和真实交互的Wasserstein距离作为信息量指标，从而计算采样概率，改进采样策略。

展望：如何引入跨会话信息到SSR问题中，十分值得研究。

Abstract

question作者想解决什么问题？

1）SR任务中，用户信息常常被忽略，所以难以抓住用户的长期兴趣。SSR任务中，流数据常常是单个交互而不是会话数据。

2）如何设计适合SSR的通用的reservoir。
method作者通过什么理论/模型来解决这个问题？

针对1），作者提出 Global Attributed Graph （GAG）neural network，全局属性的图神经网络。每当新数据到达时，GAG可以同时考虑全局属性和当前场景，以获得会话和用户的更全面的表示。

针对2）作者提出了 Wasserstein 存储库，帮助保存历史数据的代表性画像。
answer作者给出的答案是什么？

GAG + Wasserstein reservoir，取得了SOTA。

Introduction

why作者为什么研究这个课题？

会话推荐的发展现状：大部分会话推荐模型都专注与静态场景，“流会话”(Streaming session)的设定更贴近实际，但却很少研究。由于用户的喜好在随时间变化，所以对新数据做预测，仍然使用在原来数据上训练的静态模型是不合理的，为了更准确地捕捉用户兴趣，模型应该用最新的数据在线更新。

流推荐的发展现状：一些方法利用了存储技术解决流任务，但是它们的缺点是，交互数据都已相同概率存储到存储库中，这是一种离散的方式存储会话，有信息损失，捕捉不了连续的会话序列模式。还有一些在线学习的方法，每当新数据到来，模型就相应地更新，这会导致模型对新数据过拟合并且无法有效保留用户的长期兴趣。

只有SSRM提出了一个结合两者的解决方案，但有不足之处。
how当前研究到了哪一阶段？

SSRM。SSRM有两方面不足：1）计算信息量时，需要预先获得所有物品的隐含表示（MF方法得到的），别的方法不适用。2）模型将会话推荐的方法（GRU4Rec）和矩阵分解（MF）直接结合，这里原文是用MF计算的权重，对GRU4Rec的隐藏状态加权求和。很难学到用户和物品间更复杂的关联。

Dataset & Metric

数据来源

LastFM：http://mtg.upf.edu/static/datasets/last.fm/lastfm-dataset-1K.tar.gz

Gowalla：https://snap.stanford.edu/data/loc-gowalla.html

数据划分

给数据集 $D$ 中的会话按时间排序，分成前60%作为训练集，和后40%作为候选集。为了模拟线上的流数据输入，将候选集再划分成5个等长切片作为测试机。第一个测试机和10%的训练集作为验证集。实验中，若要预测第 $i$ 个测试集的序列行为，那么 $i$ 之前的测试集切片都用作在线训练。

重要指标

MRR@20、Recall@20

会话推荐Session-based Recommendation
- 属于序列推荐
流推荐Streaming Recommendation
- 属于在线学习Online Learning，大多数在线学习更关注新数据，往往不能记忆历史交互
- 随机采样Random Sampling 方法是为了解决 “历史遗忘“问题而提出的，它通过引入一个储存库来保存用户的长期交互。

Method

任务定义

Item embdding： $ x_i =Embed_v(v_i)$ ；User embdding： $ p_j =Embed_u(u_j)$ ；

User u 在时间步 t 的会话序列：$ S_{u,t}=[v_1,v_2,…,v_l]$

任务目标，根据用户 $u$ 的历史会话 $\{S_{u,0},S_{u,1},…,S_{u,t}\}$ 预测下一个可能交互的物品 $ v_{t+1}$

与会话推荐不同的是，这里假设所有会话 $S$ 都以很快的速度达到，所以受限于算力，必须选取高效的方式处理历史会话信息和当前会话信息。而会话推荐，没有流数据这一设定，可以同时处理用户所有序列，不必考虑效率。

GAG模型框架

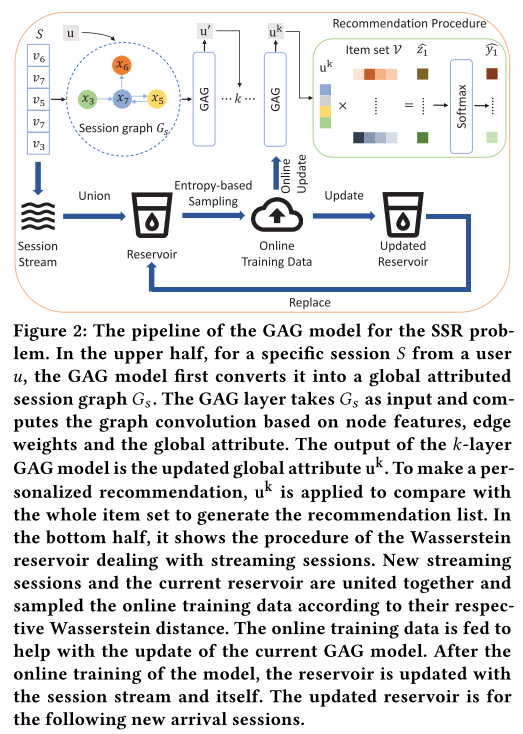
GAG的主要工作由两部分构成，1）GAG model：将用户信息转化为全局属性并将其融入到会话图中；2）Wasserstein reservoir存储库策略用来学习流数据。

Global Attributed Graph (GAG)

全局属性的会话图

建图方式和SRGNN一样，建成有向图，不同的是加入了 全局属性（用户属性） $u$ 变成三元组 $G_s = (u,V_s,E_s)$ ，图的边定义为：$E_s=(w_{s,(n-1)n},v_{n-1},v_n)$ ，也是三元组， $w$ 是权重，和SRGNN计算方式一样，基于该边出现的频率。

全局属性的图神经网络

会话图作为输入进到GAG模型，模型的计算从边、节点到全局属性。

逐边更新 per-edge update

边特征在这里指的是边的权值，是固定值，不是dense vector，不会更新。所以边信息只用来更新节点特征和全局特征。因为是有向图，所以对于一条边来说，需要双向更新，一个节点既作为sender，也作为receiver。更新公式：

$\begin{equation} \begin{aligned} e_{k,in}' &= \phi ^e_{in}(e_k,v_{r_k},v_{s_k},u) \\&= w_k \cdot MLP(v_{s_k}||u), \\ e_{k,out}' &= \phi ^e_{out}(e_k,v_{r_k},v_{s_k},u) \\&= w_k \cdot MLP(v_{s_k}||u), \end{aligned} \end{equation}$

其中两个MLP是不共享权重的，因为含义不同，一个是计算sender方向的特征，一个是计算receiver方向的特征。

逐点更新 per-node update

逐点更新是基于逐边更新的结果的。逐点更新的结果是包含所有入or出的邻居信息的标准化后的加和。以第一个公式为例， $s_j$ 是所有指向 $r_i$（也即 $i$ ）的邻居。节点 $i$ 的节点的 in-coming feature 是所有指向 $i$ 的边的标准化后的 out-going feature 的加和。标准化是将 $j$ 指向 $i$ 的这条边的 out-going feature 除以 $\sqrt{i的入度 \cdot j的出度}$ ，可以看出， $j$ 的出度越大（从 $j$ 发出的边越多），$i$ 的入度越大（指向 $i$ 的边越多），都会导致 $i$ 来自节点 $j$ 的 in-coming feature 值越小。这是符合直觉的。

$\begin{equation} \begin{aligned} v_{i,in}' =\sum_{j \in \{ v_{s_j} = v_{r_i}\}} \frac{e_{j,out'}}{\sqrt{N_{in}(i)N_{out}(j)}} \\ v_{i,out}' =\sum_{j \in \{ v_{r_j} = v_{s_i}\}} \frac{e_{j,in'}}{\sqrt{N_{out}(i)N_{in}(j)}} \end{aligned} \end{equation}$

节点的最终表示

最后节点 $i$ 表示融合了自己的 in-coming feature 和 out-going feature，节点最后的表示实际上包含了 1）自身的节点信息；2）邻居信息（通过边传播）；3）连接的边的权重；4）全局属性：

$v_i'= MLP (v_{i,in}' || v_{i,out}')$

会话表示

与NARM、STAMP、SRGNN工作类似，也用序列中的最后一个节点对其它节点做 self-attention 。有的工作用内积计算最后一个节点与其他节点的相似度作为权重，如NARM；也有用MLP获得权重的，如STAMP、SRGNN。这里用MLP。

$\begin{equation} \begin{aligned} \\ u' &= \phi ^ u (V',u) \\ &= Self-Atten(v_l',v_i',u) + u \end{aligned} \end{equation}$

Self-Atten 分为以下两个部分：

$\begin{equation} \begin{aligned} \alpha _i &= MLP(v_l'||v_i'||u) \\ u_{s,g} &= \sum ^n _{i=1} \alpha_i v_i' \end{aligned} \end{equation}$

这样得到的 $u_{s,g}$ 可以看作short-term兴趣增强的会话表示，再融合全局属性 $u$ ，得到长短期兴趣结合的会话表示： $u’ = u_{s,g} + u$ 。这种residual connection残差连接的方式，还可以减轻直接学习全局属性 $u$ 的负担。

Wasserstein Reservoir

将离线模型拓展到流设定下，提出Wasserstein reservoir方法。提出该方法的目标是：用新来的数据更新模型，并且保持从历史交互中学到的知识。

传统的在线学习方法通常只用新数据更新模型，所以导致模型会忘记过去的知识。为了避免这一点，本文利用reservoir来保持对历史数据的长期记忆，reservoir技术在流数据库管理系统中非常常见。

如何选择reservoir中的数据？之前的方法是：使用随机采样方法。每个新数据都以 $\frac{|C|}{t}$ 的概率随机替换掉已经在 $C$ 中的数据。这种方法被证明是从当前数据集中随机采样，并且可以保持模型的long-term memory。

作者认为，使用以上的随机采样方法得到 $C$ ，把它当作训练数据来训练模型的方式不好，原因如下：随机采样难以更关心新数据（time descent probability），但是最近的数据又是非常重要的。所以应该用新来的数据和reservoir $C$ 中的老数据一起更新预训练的模型，而不光光是reservoir $C$ 中的老数据。

但是，即便用新老数据一起更新模型，由于随机采样策略没变，训练数据中的大部分数据都是long-term数据，模型早就学得很好了，所以用它来训练对模型更新帮助不大。

如果当前模型在最新会话上预测结果不好，可能意味着用户兴趣转移or当前模型无法捕捉一些转换模式。这样的数据称之为”有信息量的数据“，对模型更新意义更大。

在本文中，一个会话的信息量被定义为模型预测的分布 $\hat y$ 和真实交互 $y$ 的距离。下面是三种计算距离的算法：

Wasserstein 距离（EMD 距离）：

$d_{W}\left(\mathbb{P}_{r}, \mathbb{P}_{g}\right)=\inf _{\gamma \in \Pi\left(\mathbb{P}_{r}, \mathbb{P}_{g}\right)} \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|]$

Kullback-Leibler（KL）散度：

$d_{K L}\left(\mathbb{P}_{r} \| \mathbb{P}_{g}\right)=\sum_{i=1}^{n} P_{r}(x) \log \frac{P_{r}(x)}{P_{g}(x)}$

Total Variation（全变分）距离：

$d_{T V}\left(\mathbb{P}_{r}, \mathbb{P}_{g}\right)=\sup _{A \in \Sigma}\left|\mathbb{P}_{r}(A)-\mathbb{P}_{g}(A)\right|$

在推荐任务中，真实分布是one-hot向量，只有真实标签处为1。

KL散度，也称交叉熵、相对熵。不选择KL散度的原因是：在推荐任务中，公式简化为：$d_{K L}(\mathbf{y} | \hat{\mathbf{y}})=-\log P_{g}\left(v_{i}\right)$ ，实际上只衡量了真实标签处的差异，没有考虑整个分布之间的差异。而且KL散度本身就是非对称性函数：$D(p | q) \neq D(q | p)$ ，用它作为一个真正的距离度量可能不是很合适。

不选择全变分距离的原因是：在推荐任务中，公式简化为： $d_{T V}(\mathbf{y}, \hat{\mathbf{y}})=\max _{j \neq i}\left(1-P_{g}\left(v_{i}\right), P_{g}\left(v_{j}\right)\right)$ ，这个结果要么只衡量了真实标签以外的差异，要么只衡量了真实标签。

在线训练算法描述

$S$ 是用来更新模型的，与 $C$ 无关。

因为流数据中会有新用户和新物品出现，为了防止模型忽略这些新的会话，它们会被直接加入 $S$ 当作训练数据。

$C \cup C^{n e w} - S$ 即其余的会话数据，分别计算它们的Wasserstein距离，再根据以下公式计算各自的采样概率：

$p_{\text {sample }}\left(s_{i}\right)=\frac{d_{i}}{\sum_{s_{j} \in C \cup C^{n e w}-S} d_{j}},$

采样完以后就得到训练数据 $S$ ，这个 $S$ 是对当前模型来说信息量最大的数据集，用它来更新模型最有效。

最后还要更新 reservoir $C$ ，用随机采样算法来更新，以保持模型的 long-term 记忆。

模型训练

$ Cross \ Entropy \ Loss=-\sum_{i=1}^{l} \mathrm{y}_{i} \log \left(\hat{\mathrm{y}}_{i}\right) $

Experiment & Table

对比实验结果

S-POP居然比GRU4Rec结果好，可能因为S-POP能抽取出会话间的信息。

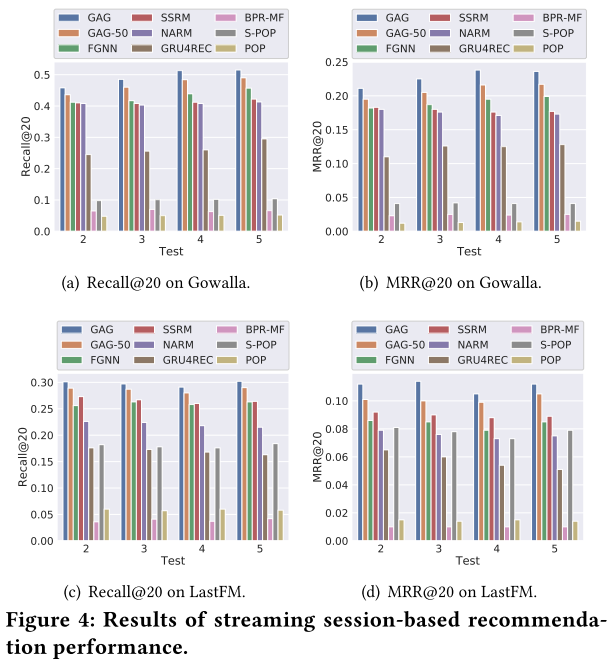
细化评价指标的top k

SSRM方法相比于另外三个基于图的方法，效果下降得幅度更大，说明图结构更适合做会话表示任务，也说明图结构有一定的泛化能力。

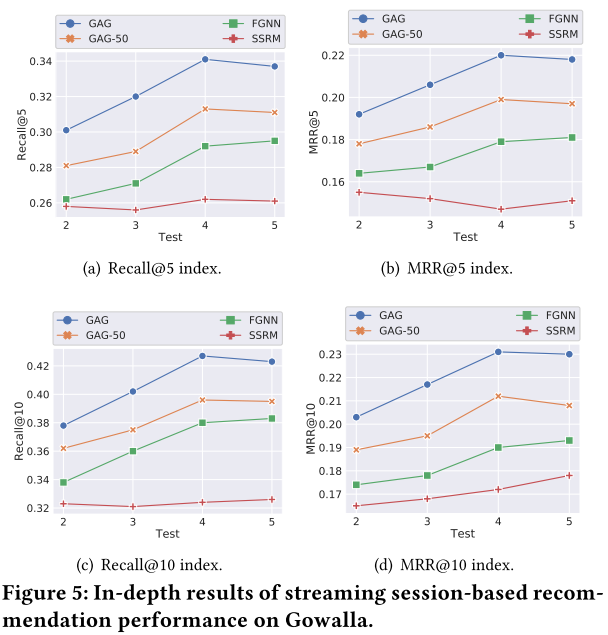
全局属性的影响

三个消融实验的对比模型如下：

FGNN：节点更新层和输出层都不加入用户信息。
GAG-FGNN：将节点更新函数换成FGNN的节点更新层，但是保留全局属性更新 $u’ = u_{s,g} + u$ 。
GAG-NoGA：节点更新层不变，但是去掉全局属性更新函数 $u’ = u_{s,g} + u$ 。

结果如下。GAG-FGNN和GAG-NoGA都在模型中融入了全局信息，前者在用户信息更新部分，后者在GNN的节点更新部分。相比于没有全局信息的FGNN，两者都有提升，说明融入全局信息对推荐是有用的。GAG-NoGA比GAG-FGNN提升更大，说明在节点更新阶段融入全局信息更有效。

Wasserstein Reservoir的影响

消融实验的对比模型如下：

GAG-Static：直接去掉在线训练部分
GAG-RanUni：从原reservoir和新数据的并集里，随机采样。这也是最普遍的设计。
GAG-FixNew：直接保留新数据，剩下的数据随机采样。
GAG-WassUni：对所有原reservoir和新数据计算Wasserstein距离，然后根据这个距离采样。（原模型是先全部保存所有带有新用户和新物品的会话，再根据Wass距离采样）

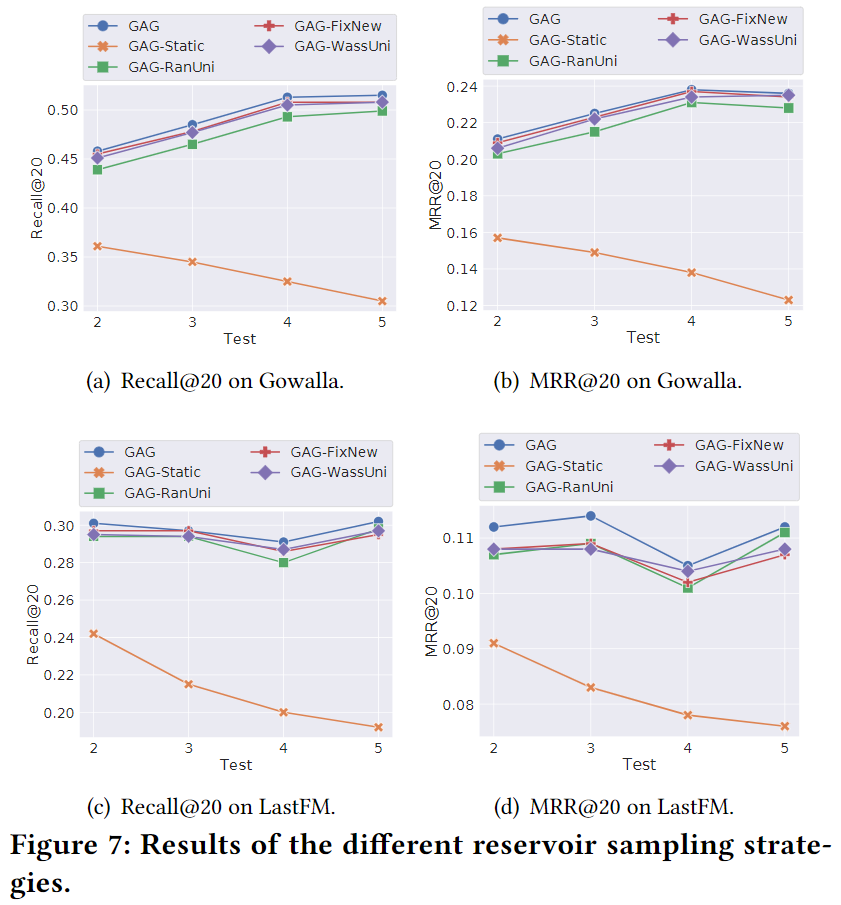
结果如下：

Static结果最差，因为：1）兴趣漂移；2）新用户、新物品出现。

纯随机采样的GAG-RanUni，在在线模型中结果最差，不如有策略地选择。

GAG-WassUni优于大部分策略，说明采用Wass距离的有效性。

GAG和GAG-WassUni相比，GAG结果更好，说明保留新用户和新物品的重要性。

Reservoir 效率分析

有两个参数reservoir的设计影响很大：reservoir大小（ $C$ ）和窗口大小（ $S$ ）。一方面，reservoir的大小表示reservoir的容量，这决定了推荐系统在线更新的存储要求。另一方面，窗口大小限制了多少数据实例将被抽样用于在线训练，这代表了推荐系统在线更新的工作负荷。

Reservoir size 的影响

Reservoir容量越大，新数据保存的概率就越低，模型就更注重历史数据。但是在流设定下，新数据更能代表用户最近的兴趣。SOTA模型SSRM在$\frac{|D|}{20}$ 时表现最好，而GAG是 $\frac{|D|}{100}$ ，所以GAG效率更高。

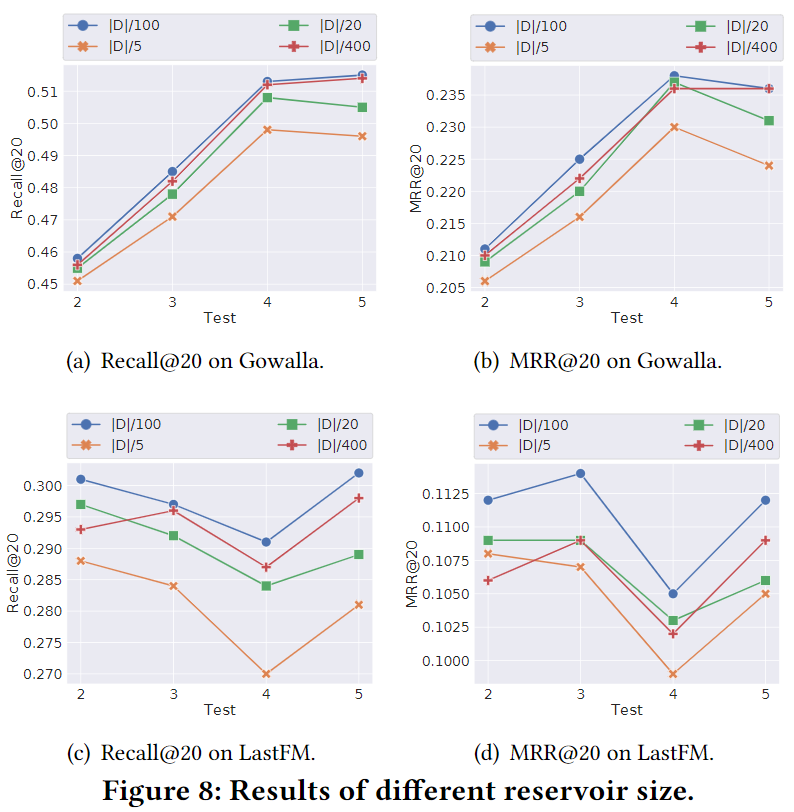
Window size 的影响

很明显，窗口大小越大，模型表现越好。

超参数的影响

Embedding size影响

GNN layer层数影响

一般来说，由于梯度爆炸，GNN模型总是受到模型深度增加的影响。在我们的实验中，GAG模型的性能随着GNN 层数增加而下降，这与常见的观察是一致的。此外，会话的连通性比传统的图数据要小，这也限制了更深的GNN模型的能力。

瓜斯拉的逆袭

论文笔记：《GAG：Global Attributed Graph Neural Network for Streaming Session-based Recommendation》

Abstract

Introduction

Dataset & Metric

Method